今天python培训分享给大家的是python中整型不会溢出的相关问题，从可行性分析、保存形式、运算等进行深入剖析，希望你学有所获!（本次分析基于 CPython 解释器，python3.x版本）

在python2时代，整型有 int 类型和 long 长整型，长整型不存在溢出问题，即可以存放任意大小的整数。在python3后，统一使用了长整型。这也是吸引科研人员的一部分了，适合大数据运算，不会溢出，也不会有其他语言那样还分短整型，整型，长整型...因此python就降低其他行业的学习门槛了。

那么，不溢出的整型实现上是否可行呢?

不溢出的整型的可行性

尽管在 C 语言中，整型所表示的大小是有范围的，但是 python 代码是保存到文本文件中的，也就是说，python代码中并不是一下子就转化成 C 语言的整型的，我们需要重新定义一种数据结构来表示和存储我们新的“整型”。

怎么来存储呢，既然我们要表示任意大小，那就得用动态的可变长的结构，显然，数组的形式能够胜任:

[

longintrepr

.

h

]

struct

_longobject

{

PyObject_VAR_HEAD

int

*

ob_digit

;

};

长整型的保存形式

长整型在python内部是用一个 int 数组( ob_digit[n] )保存值的. 待存储的数值的低位信息放于低位下标, 高位信息放于高下标.比如要保存 123456789 较大的数字,但我们的int只能保存3位(假设):

ob_digit

[

0

]

=

789

;

ob_digit

[

1

]

=

456

;

ob_digit

[

2

]

=

123

;

低索引保存的是地位，那么每个 int 元素保存多大的数合适?有同学会认为数组中每个int存放它的上限(2^31 - 1)，这样表示大数时，数组长度更短，更省空间。但是，空间确实是更省了，但操作会代码麻烦，比方大数做乘积操作，由于元素之间存在乘法溢出问题，又得多考虑一种溢出的情况。

怎么来改进呢?在长整型的 ob_digit 中元素理论上可以保存的int类型有 32 位，但是我们只保存 15位，这样元素之间的乘积就可以只用 int 类型保存即可, 对乘积结果做位移操作就能得到尾部和进位 carry了，因此定义位移长度为 15：

#define

PyLong_SHIFT

15

#define

PyLong_BASE

((

digit

)

1

<<

PyLong_SHIFT

)

#define

PyLong_MASK

((

digit

)(

PyLong_BASE

-

1

))

PyLong_MASK 也就是 0b111111111111111 ,通过与它做位运算 与 的操作就能得到低位数。

有了这种存放方式，在内存空间允许的情况下，我们就可以存放任意大小的数字了。

长整型的运算

加法与乘法运算都可以使用我们小学的竖式计算方法，例如对于加法运算:

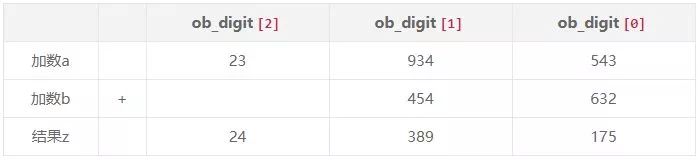
为方便理解，表格展示的是数组中每个元素保存的是 3 位十进制数，计算结果保存在变量z中，那么 z 的数组最多只要 size_a+1 的空间(两个加数中数组较大的元素个数 + 1)，因此对于加法运算，处理过程就是各个对应位置的元素进行加法运算，计算过程就是竖式计算的方式:

[

longobject

.

c

]

static

PyLongObject

*

x_add

(

PyLongObject

*

a

,

PyLongObject

*

b

)

{

int

size_a

=

len

(

a

),

size_b

=

len

(

b

);

PyLongObject

*

z

;

int

i

;

int

carry

=

0

;

// 进位

// 确保a是两个加数中较大的一个

if

(

size_a

<

size_b

)

{

// 交换两个加数

swap

(

a

,

b

);

swap

(&

size_a

,

&

size_b

);

}

z

=

_PyLong_New

(

size_a

+

1

);

// 申请一个能容纳size_a+1个元素的长整型对象

for

(

i

=

0

;

i

<

size_b

;

++

i

)

{

carry

+=

a

->

ob_digit

[

i

]

+

b

->

ob_digit

[

i

];

z

->

ob_digit

[

i

]

=

carry

&

PyLong_MASK

;

// 掩码

carry

>>=

PyLong_SHIFT

;

// 移除低15位, 得到进位

}

for

(;

i

<

size_a

;

++

i

)

{

// 单独处理a中高位数字

carry

+=

a

->

ob_digit

[

i

];

z

->

ob_digit

[

i

]

=

carry

&

PyLong_MASK

;

carry

>>=

PyLong_SHIFT

;

}

z

->

ob_digit

[

i

]

=

carry

;

return

long_normalize

(

z

);

// 整理元素个数

}

这部分的过程就是，先将两个加数中长度较长的作为第一个加数，再为用于保存结果的 z 申请空间，两个加数从数组从低位向高位计算，处理结果的进位，将结果的低 15 位赋值给 z 相应的位置。最后的 long_normalize(z)是一个整理函数，因为我们 z 申请了 a_size+1 的空间，但不意味着 z 会全部用到，因此这个函数会做一些调整，去掉多余的空间，数组长度调整至正确的数量。

若不方便理解，附录将给出更利于理解的 python 代码。

竖式计算不是按个位十位来计算的吗，为什么这边用整个元素?

竖式计算方法适用与任何进制的数字，我们可以这样来理解，这是一个 32768 (2的15次方) 进制的，那么就可以把数组索引为 0 的元素当做是 “个位”，索引 1 的元素当做是 “十位”。

乘法运算

乘法运算一样可以用竖式的计算方式，两个乘数相乘，存放结果的 z 的元素个数为 size_a+size_b即可：

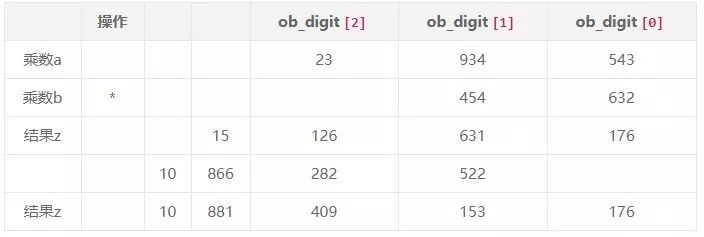
这里需要主意的是，当乘数 b 用索引 i 的元素进行计算时，结果 z 也是从 i 索引开始保存。先创建 z 并初始化为 0，这 z 进行累加，加法运算则可以利用前面的 x_add 函数：

// 为方便理解，会与cpython中源码部分稍有不同

static

PyLongObject

*

x_mul

(

PyLongObject

*

a

,

PyLongObject

*

b

)

{

int

size_a

=

len

(

a

),

size_b

=

len

(

b

);

PyLongObject

*

z

=

_PyLong_New

(

size_a

+

size_b

);

memset

(

z

->

ob_digit

,

0

,

len

(

z

)

*

sizeof

(

int

));

// z 的数组清 0

for

(

i

=

0

;

i

<

size_b

;

++

i

)

{

int

carry

=

0

;

// 用一个int保存元素之间的乘法结果

int

f

=

b

->

ob_digit

[

i

];

// 当前乘数b的元素

// 创建一个临时变量，保存当前元素的计算结果，用于累加

PyLongObject

*

temp

=

_PyLong_New

(

size_a

+

size_b

);

memset

(

temp

->

ob_digit

,

0

,

len

(

temp

)

*

sizeof

(

int

));

// temp 的数组清 0

int

pz

=

i

;

// 存放到临时变量的低位

for

(

j

=

0

;

j

<

size_a

;

++

j

)

{

carry

=

f

*

a

[

j

]

+

carry

;

temp

[

pz

]

=

carry

&

PyLong_MASK

;

// 取低15位

carry

=

carry

>>

PyLong_SHIFT

;

// 保留进位

pz

++;

}

if

(

carry

){

// 处理进位

carry

+=

temp

[

pz

];

temp

[

pz

]

=

carry

&

PyLong_MASK

;

carry

=

carry

>>

PyLong_SHIFT

;

}

if

(

carry

){

temp

[

pz

]

+=

carry

&

PyLong_MASK

;

}

temp

=

long_normalize

(

temp

);

z

=

x_add

(

z

,

temp

);

}

return

z

}

这大致就是乘法的处理过程，竖式乘法的复杂度是n^2，当数字非常大的时候(数组元素个数超过 70 个)时，python会选择性能更好，更高效的 Karatsuba multiplication 乘法运算方式，这种的算法复杂度是 3nlog3≈3n1.585，当然这种计算方法已经不是今天讨论的内容了。有兴趣的小伙伴可以去了解下。

总结

要想支持任意大小的整数运算，首先要找到适合存放整数的方式，本篇介绍了用 int 数组来存放，当然也可以用字符串来存储。找到合适的数据结构后，要重新定义整型的所有运算操作，本篇虽然只介绍了加法和乘法的处理过程，但其实还需要做很多的工作诸如减法，除法，位运算，取模，取余等。

python代码以文本形式存放，因此最后，还需要一个将字符串形式的数字转换成这种整型结构:

[

longobject

.

c

]

PyObject

*

PyLong_FromString

(

const

char

*

str

,

char

**

pend

,

int

base

)

{

}

这部分不是本篇的重点，有兴趣的同学可以看看这个转换的过程，这个过程还是比较繁琐的，因为它还要处理进制问题,能够处理 0xfff3 或者 0b1011 等情况。

参考

https

:

//github.com/python/cpython/blob/master/Objects/longobject.c

附录

# 例子中的表格中，数组元素最多存放3位整数，因此这边设置1000

# 对应的取低位与取高位也就变成对 1000 取模和取余操作

PyLong_SHIFT

=

1000

PyLong_MASK

=

999

# 以15位长度的二进制

# PyLong_SHIFT = 15

# PyLong_MASK = (1 << 15) - 1

def

long_normalize

(

um

):

"""

去掉多余的空间，调整数组的到正确的长度

eg: [176, 631, 0, 0] ==> [176, 631]

:param num:

:return:

"""

end

=

len

(

um

)

while

end

>=

1

:

if

um

[

end

-

1

]

!=

0

:

break

end

-=

1

um

=

um

[:

end

]

return

um

def

x_add

(

a

,

b

):

size_a

=

len

(

a

)

size_b

=

len

(

b

)

carry

=

0

# 确保 a 是两个加数较大的，较大指的是元素的个数

if

size_a

<

size_b

:

size_a

,

size_b

=

size_b

,

size_a

a

,

b

=

b

,

a

z

=

[

0

]

*

(

size_a

+

1

)

i

=

0

while

i

<

size_b

:

carry

+=

a

[

i

]

+

b

[

i

]

z

[

i

]

=

carry

%

PyLong_SHIFT

carry

//= PyLong_SHIFT

i

+=

1

while

i

<

size_a

:

carry

+=

a

[

i

]

z

[

i

]

=

carry

%

PyLong_SHIFT

carry

//= PyLong_SHIFT

i

+=

1

z

[

i

]

=

carry

# 去掉多余的空间，数组长度调整至正确的数量

z

=

long_normalize

(

z

)

return

z

def

x_mul

(

a

,

b

):

size_a

=

len

(

a

)

size_b

=

len

(

b

)

z

=

[

0

]

*

(

size_a

+

size_b

)

for

i

in

range

(

size_b

):

carry

=

0

f

=

b

[

i

]

# 创建一个临时变量

temp

=

[

0

]

*

(

size_a

+

size_b

)

pz

=

i

# 元素计算结果从 i 索引开始保存

for

j

in

range

(

size_a

):

carry

+=

f

*

a

[

j

]

temp

[

pz

]

=

carry

%

PyLong_SHIFT

carry

//= PyLong_SHIFT

pz

+=

1

if

carry

:

carry

+=

temp

[

pz

]

temp

[

pz

]

=

carry

%

PyLong_SHIFT

carry

//= PyLong_SHIFT

pz

+=

1

if

carry

:

temp

[

pz

]

+=

carry

%

PyLong_SHIFT

temp

=

long_normalize

(

temp

)

z

=

x_add

(

z

,

temp

)

return

z

a

=

[

543

,

934

,

23

]

b

=

[

632

,

454

]

print

(

x_add

(

a

,

b

))

print

(

x_mul

(

a

,

b

))

恭喜你阅读完了本文，此刻你已经了解了python中整型不会溢出的相关的问题，不知道你是否已经完全理解?如果还有问题，欢迎你来达内python培训机构进行咨询。

免责声明：内容和图片源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。