Python培训
400-996-5531
使用Python代码解决规划雨水问题
首先要解决使用python规划出雨水问题就要知道这个问题是什么，下面先看一下问题描述，给定n个非负整数表示每个宽度为1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水?下面作出了两种解答，希望能够帮助到大家。
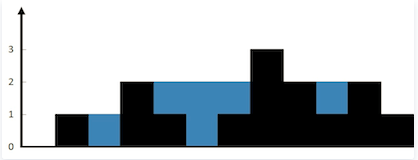
图1.1 问题示意图
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水(蓝色部分表示雨水)。
解决方案：
首先来理解题意，3能接到水是因为左边最高高度是1右边最高高度是3原本高度是零，可以得到在3的位置能接到水的量是左右最高中最小的减去原本的，然后把所有能接到的水合起来就是答案。
1、普通代码(暴力便捷但超时)
def trap(height):
ans = 0
for i in range(len(height)):
max_left, max_right = 0, 0
# 寻找 max_left
for j in range(0, i):
max_left = max(max_left, height[j])
# 寻找 max_right
for j in range(i, len(height)):
max_right = max(max_right, height[j])
if min(max_left, max_right) > height[i]:
ans += min(max_left, max_right) - height[i]
return ans
height=[0,1,0,2,1,0,1,3,2,1,2,1]
print(trap(height))
2、动态规划代码
上述题意符合动态规划的3要素优子结构、边界和状态转移，而且在寻找每个下标的左边和右边最高的柱子时，会对柱子进行反复搜索导致复杂度降低，假如使用两个数组lmax和rmax，lmax[i]表示下标i左边最高柱子的高度,rmax[i] 表示下标i右边最高柱子的高度，很明显，只需要一趟遍历就可以得到结果。这样由于避免了重复计算，就避免了超时。
def trap(height):
#边界条件
if len(height)<3:
return 0
n=len(height)
lmax=[0]*n
rmax=[0]*n
ans=0
#初始化左右峰
lmax[0]=height[0]
rmax[n-1]=height[n-1]
#储存左右峰
for i in range(1,n):
lmax[i]=max(height[i],lmax[i-1])
for j in range(n-2,-1,-1):
rmax[j]=max(height[j],rmax[j+1])
#遍历 比较每个位置可以存多少水
for k in range(n):
if min(rmax[k],lmax[k])>height[k]:
ans+=min(rmax[k],lmax[k])-height[k]
return ans
height=[0,1,0,2,1,0,1,3,2,1,2,1]
print(trap(height))
结语
综上所述，只要具备以上三要素的问题均可以采用动态规划的策略进行求解，动态规划可以有效的减少代码的时间复杂度提高代码可读性，是我们编程的好帮手，要熟练掌握。
版权声明：转载文章来自公开网络，版权归作者本人所有，推送文章除非无法确认，我们都会注明作者和来源。如果出处有误或侵犯到原作者权益，请与我们联系删除或授权事宜。
预约申请免费试听课
填写下面表单即可预约申请免费试听！ 怕学不会？助教全程陪读，随时解惑！担心就业？一地学习，可全国推荐就业！
下一篇：Python回溯法：火柴拼正方形
Copyright © Tedu.cn All Rights Reserved 京ICP备08000853号-56 
京公网安备 11010802029508号 达内时代科技集团有限公司 版权所有
选择城市和中心
北京
黑龙江省
吉林省
内蒙古
河北省
陕西省
江苏省
湖北省
四川省
重庆
湖南省
江西省
贵州省
云南省
广西省
海南省
台湾