


Python培训
400-996-5531
拉普拉斯方程是一种最简单的二阶偏微分方程,同样也是一种最简单的椭圆形偏微分方程。此方程在科学界,尤其是物理学上具有举足轻重的地位,因为它能够描述电势能和热传导问题。在热力学(热传导)中,我们将拉普拉斯方程称为稳态热方程或者热传导方程。
在这篇文章中,我们将用数值求解代替积分求解,来求解拉普拉斯方程。当我们一提到数值方法,就意味着离散化。离散化就是将连续形式的微分方程转化为离散形式,同时它意味着我们将积分问题转化为线性代数问题,以便使用程序解决。
在这篇文章中,我们使用有限差分法来求解简单的热传导问题。我们的编程语言是 Python,使用的库有:Numpy(numerical library for Python) 和 matplotlib(library for plotting and visualizing data using Python)。下面将看到,我们可以使用很少的 Python 代码来实现丰富的功能。
背景
在计算物理中,我们经常编程来解决问题,因为计算机程序可以进行大型且复杂的计算。计算物理领域就像下图所展示的一样:
现如今,有很多编程语言可以进行数值计算,例如 MATLAB。但是此处我们使用 Python,因为它简单易学而且还免费。它有很多非常好用的数值计算和数据可视化库,例如 Numpy,Scipy 和 Matplotlib。Python 也提供可以实现并行计算,我们可以在计算机集群上运行 Python 程序。
让我们回到拉普拉斯方程上,下一节我们将使用 Python 来计算简单的二维热传导方程。首先我们默认读者们已经了解了关于有限差分法的基本理论知识,此处我不再详细介绍有限差分法的内容,离散化带来的误差问题,稳定性问题,一致性问题,收敛问题以及测试优化问题等我也不详细说明。同样,我们也将会跳过很多计算公式。
此处我们关注的只是如何使用 Python,Numpy 和 Matplotlib 来解决问题,当然也捎带的讲述一点计算的物理意义,但是我们不会过多的关注数值分析验证问题。所以下面给出的源代码对那些不懂计算物理学的读者来说是有价值的。
准备工作
我们的实验环境:
系统 OS: Linux Ubuntu 14.04 LTS
Python: Python 2.7
Numpy: Numpy 1.10.4
Matplotlib: Matplotlib 1.5.1
如果你使用的是 Ubuntu 系统,你可以使用 pip 来安装 Numpy 和 Matplotlib,或者在你的终端上运行下面的语句:
用下面的语句安装 Matplotlib
注意一点: Ubuntu 14.04 系统自带 Python,你只需要在你的终端输入 Python 然后按回车键即可。
当然我们可以在 Windows 操作系统上使用 Python,Numpy 和 Matplotlib,但是我更喜欢 Ubuntu。
编写代码
下式即为二维热传导问题的拉普拉斯方程
其中 T 代表了温度,x 代表 x 轴,y 代表了 y 轴。x 和 y分别是位置坐标的函数。如果你想看这个方程的积分解,可以点击这里。
此处我们仅仅求解二维的拉普拉斯方程。求解过程如下:
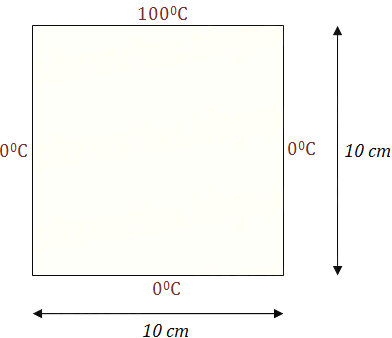
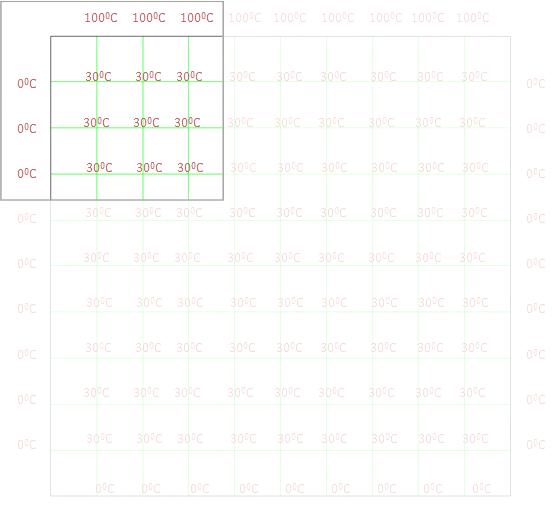
我们求解的问题是:在给定边界温度的情况下,求出二维平面内每点的稳定温度(即为拉普拉斯方程的解)。下面,我们将离散化整个二维平面,使用方格将其分割,然后使用有限差分法将拉普拉斯方程进行离散化。下图展示了离散化后的平面区域。
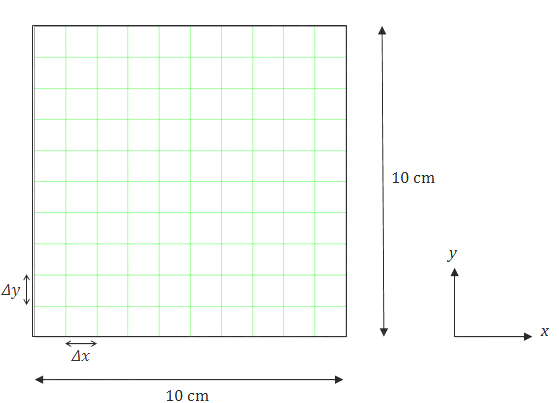
我们设置 Δx = Δy = 1 cm,得到如下的方格图。
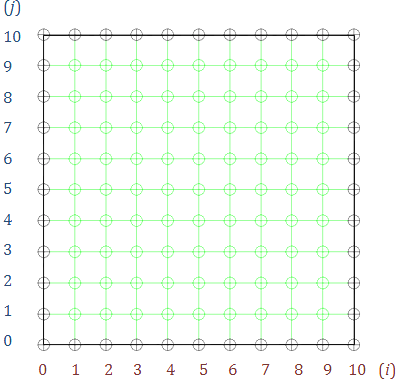
其中,绿色的节点代表了我们想求解的节点,白色的节点是边界条件,我们已知其温度。下面给出离散化的拉普拉斯方程形式。
将上式整理后,可以得到最终的离散方程如下所示。
下面让我求解这个方程。为了求解这个方程,首先使用为所有的绿色节点假设一个猜测值,此处的猜测值是 30 摄氏度,当然你也可以设置为 35 摄氏度,因为我们并不知道其具体是多少度,这只是一个假设值。我们将迭代这个方程,直到迭代前后值的误差非常小为止,我们称之为收敛。在迭代的过程中,节点的温度值会自动的调整,所以当我们的猜测值越接近真实值,求解的速度就越快。
下面让我们正式开始写代码。为了使用 Numpy,我们需要将其载入,同样的过程适用于 Matplotlib。 我们使用 pyplot 模块来画最后的结果。所以,第一步是载入必要的模块。
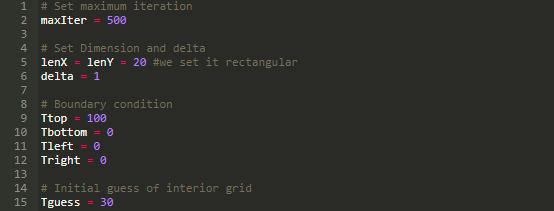
然后,我们为程序设置变量初始值。
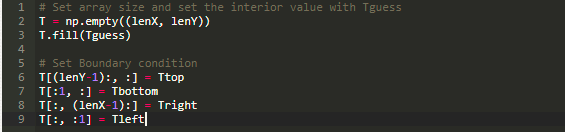
然后就是设置画图窗口,并将其分割。

np.meshgrid() 函数可以产生网格,用这个可以画出最后的结果,其中第一个参数代表 x 轴,第二个参数代表了 y 轴。我们使用 p.arange() 来产生一个一维数组,其起始于某一个值,终止于某一个值,在本例中,起始于 0 终止于 lenX,另一个起始于 0 终止于 lenY。接下来,我们生成一个二维数组,定义其形状,并使用猜测值对其进行初始化,然后我们设置边界条件,使用前面给出的边界条件进行初始化。
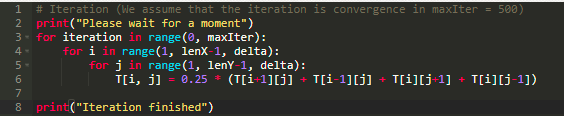
然后我们使用 Python 来实现方程,并在 for 循环中对其进行迭代。
注意代码的缩进格式,Python 代码使用的是空格或者缩进,而不使用大括号。截止此处,我们的主程序部分已经完成了,接下来,我们使用 Matplotlib 来画出最后的结果。
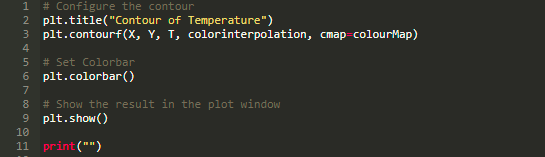
完成! 下面给出完整的程序。
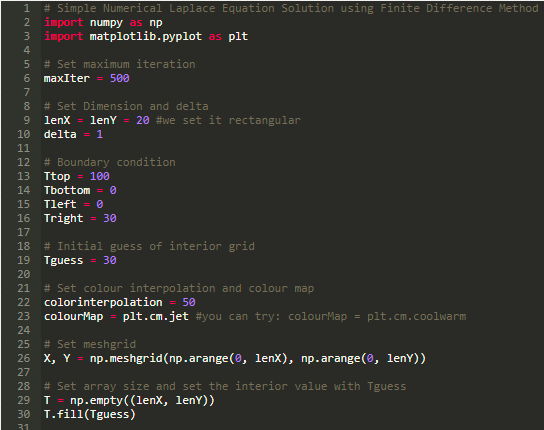
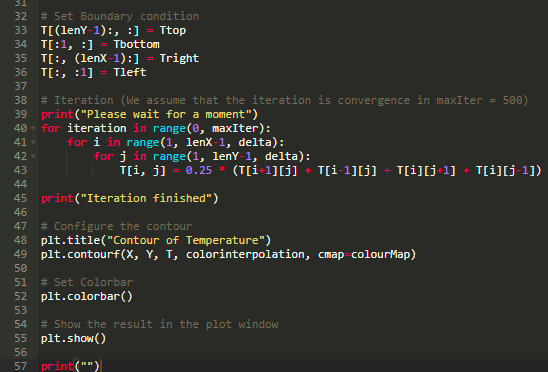
程序很短,对吧。 好的,下面我们将程序复制粘贴到名为 findif.py 的文件中。然后打开终端,进入源代码所在目录,使用下面的语句运行程序。
运行后,我们会得到下面的结果图。
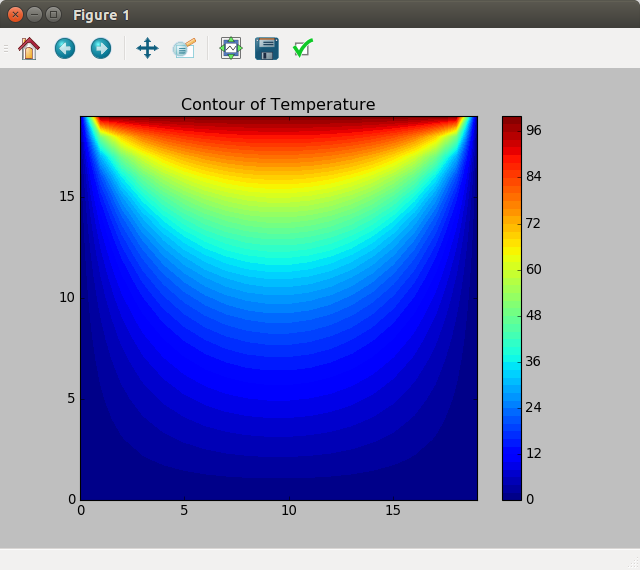
我们可以改变边界条件,例如将右侧边界的值设置为 30 摄氏度,即 Tright = 30,会得到下面的结果图。

兴趣点
Python 是一种简单易学的动态编程语言,在计算物理和别的学科里,它有很多有用的库。因为 Python 是一种解释型的语言,和 C 、 C++ 相比,它可能运行的比较慢,但是必须强调的是,它很好学。我们同样可以使用较少的 Python 代码来实现更多的工作。这样一来,我们不必纠结于如何编程,只需将精力放在想要解决的问题上面。
在计算物理中,使用 Numpy 和 Scipy(numeric and scientific library for Python)我们可以解决很多复杂的问题,因为这些库为我们提供了矩阵运算,线性代数操作以及信号处理,傅里叶变化,统计分析,优化等等现成的函数。
另外,不仅在计算物理领域, Python 还广泛的应用于机器学习,甚至谷歌的 tensorflow 也用的是 Python。
填写下面表单即可预约申请免费试听! 怕学不会?助教全程陪读,随时解惑!担心就业?一地学习,可全国推荐就业!
Copyright © Tedu.cn All Rights Reserved 京ICP备08000853号-56  京公网安备 11010802029508号 达内时代科技集团有限公司 版权所有
京公网安备 11010802029508号 达内时代科技集团有限公司 版权所有