基本介绍

梯度下降法(gradient descent)，又名最速下降法(steepest descent)是求解无约束最优化问题最常用的方法，它是一种迭代方法，每一步主要的操作是求解目标函数的梯度向量，将当前位置的负梯度方向作为搜索方向。

梯度下降法特点：越接近目标值，步长越小，下降速度越慢。

下面将通过公式来说明梯度下降法。

建立模型为拟合函数h(θ) :

接下来的目标是将该函数通过样本的拟合出来，得到最佳的函数模型。因此构建损失函数J(θ)(目的是通过求解min J(θ)，得到在最优解下的θ向量)，其中的每一项

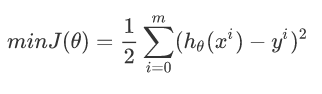
要使得最小J(θ)，则对其J(θ)求导等于零。

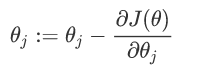
在处理以下步骤时，可以用批量梯度下降算法(BGD)与随机梯度下降算法(SGD)。

批量梯度下降算法(BGD)

单个特征

a为步长，如果太小，则找到函数最小值的速度就很慢，如果太大，则可能会错过最小值，而使得函数值发散。初始点不同，获得的最小值也不同，因此梯度下降求得的只是局部最小值。

多个特征的迭代如下：

Repeat until convergence{

}

当上式收敛时则退出迭代，一开始设置一个具体参数，当前后两次迭代差值小于该参数时候结束迭代。

使用梯度下降法，越接近最小值时，下降速度越慢。计算批量梯度下降法时，计算每一个θ值都需要遍历计算所有样本，当数据量比较大时这是比较费时的计算。

随机梯度下降算法(SGD)

为解决数据量大的时批量梯度下降算法费时的困境。随机梯度下降算法，每次迭代只是考虑让该样本点的J(θ)趋向最小，而不管其他的样本点，这样算法会很快，但是收敛的过程会比较曲折，整体效果上，大多数时候它只能接近局部最优解，而无法真正达到局部最优解。该算法适合用于较大训练集的例子。

Loop{

for i=1 to m,{

}

}

改进的随机梯度下降算法

为了避免迭代时系数出现周期性波动，同时让系数很快收敛，这里改进随机梯度下降算法。

1)在每次迭代时，调整更新步长a的值。随着迭代的进行，a越来越小，这会缓解系数的高频波动。同时为了避免a随着迭代不断减小到接近于0，约束a一定大于一个稍微大点的常数项。

2)每次迭代，改变样本的优化顺序。也就是随机选择样本来更新回归系数。这样做可以减少周期性的波动，因为样本顺序的改变，使得每次迭代不再形成周期性。

算法应用和python实现

梯度下降法可以用于在前面提到的logistic回归分类器中，主要是求解模型中的cost函数，这里用泰坦尼克数据集进行演示，并且使用python中的sklearn库进行实现，代码如下：

import pandas

from sklearn.linear_model import LinearRegression, LogisticRegression

from sklearn.model_selection import KFold, cross_val_score

import numpy as np

titanic = pandas.read_csv('E:\TitanicData\Titanic\\train.csv')

# print(titanic.describe())

titanic['Age'] = titanic['Age'].fillna(titanic['Age'].mean())

# print(titanic.describe())

# print(titanic['Sex'].unique())

titanic.loc[titanic['Sex'] == 'male', 'Sex'] = 0

titanic.loc[titanic['Sex'] == 'female', 'Sex'] = 1

# print(titanic['Embarked'].unique())

titanic['Embarked'] = titanic['Embarked'].fillna('S')

titanic.loc[titanic['Embarked'] == 'S', 'Embarked'] = 0

titanic.loc[titanic['Embarked'] == 'C', 'Embarked'] = 1

titanic.loc[titanic['Embarked'] == 'Q', 'Embarked'] = 2

# print(titanic.columns)

predictors = ['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked']

#开始线性回归预测

alg = LinearRegression()

X = titanic[predictors]

kf = KFold(n_splits=3)

prediction = []

for train, test in kf.split(X):

x_train = titanic[predictors].iloc[train, :]

y_train = titanic['Survived'].iloc[train]

x_test = titanic[predictors].iloc[test, :]

y_test = titanic['Survived'].iloc[test]

alg.fit(x_train, y_train)

test_prediction = alg.predict(x_test)

prediction.append(test_prediction)

prediction = np.concatenate(prediction)

prediction[prediction > 0.5] = 1

prediction[prediction < 0.5] = 0

accuracy_linear = sum(prediction[prediction == titanic['Survived']])/len(prediction) #查准率

#score1 = cross_val_score(alg, X, titanic['Survived'], cv=3).mean()

# cross_val_score是直接将算法得到的值与y_test进行对比算scoring

# 这个步骤错误，因为线性回归得到的是概率值，需要后期判别到{0,1}上，才能和原y_test的数据进行比较算accuracy，所以LinearRegression不适合做cross_val_score的estimator。

print(accuracy_linear, score1)

#开始逻辑回归预测

alh = LogisticRegression()

score = cross_val_score(alh, X, titanic['Survived'], cv=3).mean()

#logisticregression的算法结果直接是{0,1}两值，所以可以直接进行score比较算accuracy，所以这个alh适合这个estimator。

print(score)

本文内容转载自网络，本着分享与传播的原则，版权归原作者所有，如有侵权请联系我们进行删除!